طراحی فیلترهای خطی در حوزه فرکانس
در این مقاله با موارد زیر آشنا خواهید شد:
- آشنایی با فیلترهای FIR
- متد تبدیل فرکانس(Frequency Transformation Method)
- متد نمونه گیری فرکانس(Frequency Sampling Method)
- متد Windowing
- ایجاد ماتریس پاسخ فرکانسی دلخواه
- محاسبه ی پاسخ فرکانسی یک فیلتر
آشنایی با فیلترهای FIR
جعبه ابزار پردازش تصویر متلب، از یک دسته از فیلترهای خطی دو بعدی به نام فیلترهای FIR (مخفف finite impulse response) پشتیبانی می کند.
تمامی توابع فیلترهای جعبه ابزار پردازش تصویر، فیلترهای FIR را برمی گردانند.فیلترهای FIR چندین خاصیت دارند که باعث می شود استفاده از آنها در پردازش تصویر متلب، ایده آل باشد.
- استفاده از فیلترهای FIR به صورت ماتریس های ضرایب، بسیارساده می باشد.
- فیلترهای دوبعدی FIR بسط طبیعی فیلترهای یک بعدی FIR می باشند.
- روش های شناخته شده ی زیادی برای طراحی فیلترهای FIR وجود دارند.
- اجرا و پیاده سازی فیلترهای FIR ساده می باشد.
- فیلترهای FIR می توانند طوری طراحی شوند که دارای فاز خطی باشند. که باعث می شود از اعوجاج اجتناب شود.
یک دسته ی دیگر از فیلترها، فیلترهای IIR (یا infinite impulse response) هستند. جعبه ابزار پردازش تصویر متلب، از فیلترهای IIR پشتیبانی نمی کند.
متد تبدیل فرکانس(Frequency Transformation Method)
متد تبدیل فرکانس، یک فیلتر یک بعدی FIR را به یک فیلتر دو بعدی FIR تبدیل می کند.
متد تبدیل فرکانس، از اکثر مشخصه های فیلتر یک بعدی محافظت می کند.
این متد، از یک ماتریس تبدیل و یک مجموعه از عناصر که مشخص کننده ی تبدیل فرکانس هستند، استفاده می کند.
از تابع ftrans2 که در جعبه ابزار پردازش تصویر متلب وجود دارد، برای اجرای متد تبدیل فرکانس استفاده می شود.
ماتریس تبدیل پیش فرض این تابع، فیلترها را با استفاده از تقارن تقریبی دایره ای(nearly circular symmetry) تولید می کند.
اگر ماتریس تبدیل دلخواه خود را به این تابع بدهید، قادر خواهید بود تا تقارن های متفاوتی را به دست بیاورید.
متد تبدیل فرکانس، به طور کلی نتایج بسیار خوبی را تولید می کند زیرا طراحی یک فیلتر یک بعدی با مشخصه های خاص آسان تر از طراحی یک فیلتر دو بعدی است.
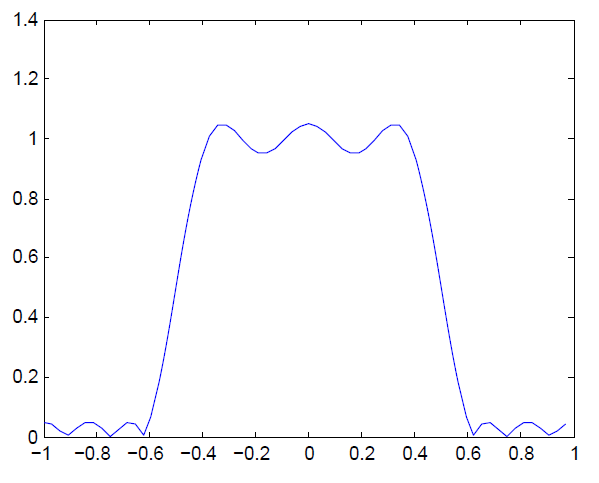
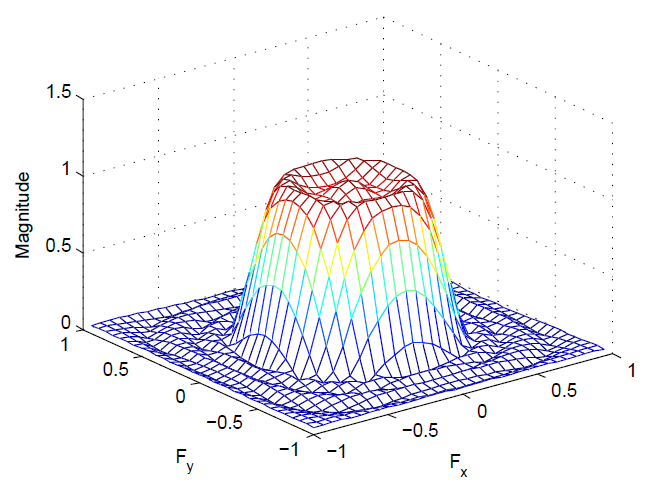
برای نمونه، در مثال زیر، یک فیلتر FIR یک بعدی بهینه طراحی شده است و از آن برای ایجاد یک فیلتر دوبعدی با همان مشخصه ها استفاده شده است.
شکل پاسخ فرکانسی یک بعدی، به وضوح در پاسخ فرکانسی دو بعدی قابل مشاهده است:
;کدها:
b = remez(10,[0 0.4 0.6 1],[1 1 0 0]);
h = ftrans2(b);
[H,w] = freqz(b,1,64,'whole');
colormap(jet(64))
plot(w/pi-1,fftshift(abs(H)))
figure, freqz2(h,[32 32])
متد نمونه گیری فرکانس(Frequency Sampling Method)
متد نمونه گیری فرکانس، بر اساس یک پاسخ فرکانسی دلخواه، یک فیلتر را ایجاد می کند.
- نوشته شده توسط احسان عباسی
- بازدید: 5139





