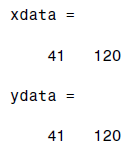در این مقاله با موارد زیر آشنا خواهید شد:
- مقدمه
- انجام یک انتقال در قالب یک مثال
- تعریف داده های تبدیلات
- ایجاد ساختارهای TFORM
- انجام تبدیلات فضایی
مقدمه
انجام تبدیلات فضایی دوبعدی اصلی شامل سه مرحله است:
1. تعریف پارامترهای تبدیلات فضایی
2. ایجاد یک ساختار تبدیلی به نام ساختار TFORM که درواقع نوع تبدیلی که شما می خواهید انجام دهید را مشخص می کند.
TFORM یک ساختار در متلب است که حاوی 3 پارامتر ضروری برای انجام یک تبدیل است. شما می توانید برای ایجاد یک ساختار TFORM از تابع maketform استفاده نمایید.
3. انجام تبدیلات مورد نظر
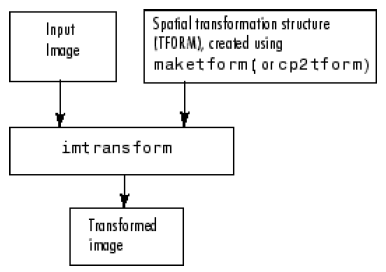
برای انجام این کار، باید عکس مورد نظر و ساختار TFORM خود را به تابع imtransform بدهید.
عکس زیر این فرآیند را نشان می دهد:
انجام یک انتقال در قالب یک مثال
این مثال نشان می دهد که چطور می توانیم از توابع maketform و imtransform برای انجام یک تبدیل دو بعدی بر روی یک عکس، استفاده کنیم. در این مثال، تبدیل affine را که یک انتقال نامیده می شود، انجام خواهیم داد. در یک انتقال، درواقع شما با اضافه کردن یک مقدار به مختصات x و y یک عکس، آن را در صفحه ی مختصات انتقال می دهید. برای انجام این کار گام های زیر را انجام دهید:
گام شماره 1: عکسی که قرار است مورد تبدیل قرار بگیرد را وارد نمایید.
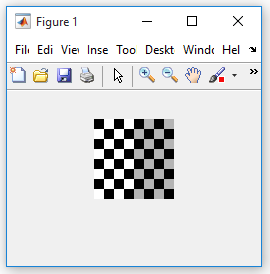
عکسی که می خواهیم مورد تبدیل قرار بگیرد را در محیط workspace وارد کنید. در این مثال ما با استفاده از تابع checkerboard یک عکس شطرنجی را ایجاد می کنیم. به طور پیش فرض، تابع checkerboard یک عکس 80 در 80 پیکسل را ایجاد می کند:
مثال (تبدیلات فضایی دو بعدی اصلی در متلب)
cb = checkerboard;
imshow(cb)
گام شماره 2: تعریف تبدیلات فضایی
اکنون شما باید تبدیلات فضایی که می خواهید انجام دهید را تعریف کنید. برای اکثر تبدیلات فضایی دو بعدی مثل تبدیلات affine، شما می توانید از یک ماتریس تبدیل 3×3 برای مشخص کردن تبدیل مورد نظر، استفاده کنید. شما همچنین می توانید مجموعه ای از نقاط را در عکس های ورودی و خروجی مورد استفاده قرار دهید تا بتوانید تبدیل خود را مشخص کنید و به تابع maketform امکان دهید تا ماتریس تبدیل را ایجاد نماید. در این مثال، از ماتریس تبدیل زیر برای تعریف یک تبدیل فضایی استفاده می شود که به آن یک انتقال می گوییم:
مثال (تبدیلات فضایی دو بعدی اصلی در متلب)
xform = [ 1 0 0
0 1 0
40 40 1 ]
در این ماتریس، مقدار (xform(3,1 مشخص کننده ی تعداد پیکسل های انتقال عکس در جهت افقی است. و مقدار (xform(3,2 مشخص کننده ی تعداد پیکسل های انتقال عکس در جهت عمودی است.
گام شماره 3: ایجاد ساختار TFORM
شما می توانید برای ایجاد یک ساختار TFORM از تابع maketform استفاده نمایید. سپس باید نوع تبدیل که می خواهید انجام دهید و ماتریس تبدیل(یا مجموعه نقاط) که ایجاد نموده اید را بعنوان آرگومان به این تابع بدهید. در مثال زیر، ابتدا تابع maketform فراخوانی می شود و برای نوع تبدیل از مقدار 'affine' استفاده می شود(بعنوان آرگومان اول) و سپس مقدار xform که در گام 2، ایجاد کردیم بعنوان آرگومان دوم به این تابع داده می شود.
مثال (تبدیلات فضایی دو بعدی اصلی در متلب)
tform_translate = maketform('affine',xform);
گام شماره 4: انجام تبدیلات مورد نظر
برای انجام تبدیلات مورد نظر، تابع imtransform را فراخوانی کنید و عکس مورد نظر و ساختار TFORM که حاوی پارامترهای تبدیلات مورد نیاز است را به این تابع بدهید. در مثال زیر، عکس شطرنجی که در گام شماره 1 ایجاد کردیم و ساختار TFORM که در گام شماره 3 ایجاد کردیم را به تابع imtransform می دهیم. و تابع imtransform عکس تبدیل شده را برمی گرداند:
مثال (تبدیلات فضایی دو بعدی اصلی در متلب)
[cb_trans xdata ydata]= imtransform(cb, tform_translate);
مثال بالا، حاوی دو آرگومان خروجی اختیاری به نام های xdata و ydata است. این آرگومان ها موقعیت عکس خروجی را در صفحه مختصات خروجی نشان می دهند. متغیر xdata حاوی مختصات x از پیکسل های گوشه های عکس خروجی است. و متغیر ydata حاوی مختصات y از همان پیکسل ها است.
نکته: این بخش هنگام اشاره کردن به پیکسل ها، از سیستم مختصات فضایی استفاده می کند. در سیستم مختصات فضایی، مختصات x و y مرکز پیکسل را مشخص می کنند.
عکس زیر، بصورت گرافیکی، تبدیل مورد نظر را نمایش می دهد. به طور قراردادی، محورهای مختصات ورودی، با u و v نشان داده می شوند و محورهای مختصات خروجی با x و y نشان داده می شوند. همان طور که در عکس زیر نشان داده شده است، پیکسل نقطه ی (1,1) در نقطه ی (41,41) قرار گرفته است. در عکس شطرنجی، هر مربع دارای 10 پیکسل ارتفاع و 10 پیکسل عرض است.
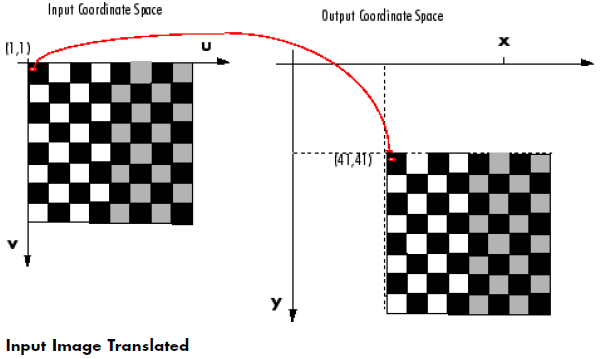
عکس بالا نشان می دهد که چگونه تابع imtransform موقعیت پیکسل های صفحه مختصات ورودی و صفحه مختصات خروجی را تغییر می دهد. همان طور که در تصویر بالا مشاهده می کنید، پیکسل قرار گرفته در نقطه ی (1,1) در عکس ورودی، به نقطه ی (41,41) در عکس خروجی انتقال یافته است. اما توجه کنید که مقدار آن پیکسل هیچ تغییری نکرده است. زیرا پیکسل قرار گرفته در نقطه ی (1,1) در عکس ورودی به رنگ سیاه است، و پیکسل قرار گرفته در نقطه ی (41,41) در عکس خروجی نیز به رنگ سیاه است.
در یک انتقال، به دلیل اینکه سایز و جهت عکس خروجی مشابه با عکس ورودی است، یک نگاشت یک به یک از مقادیر پیکسل ها در موقعیت های جدید وجود دارد. در دیگر انواع تبدیلات، مثل مقیاس دهی یا چرخش، تابع imtransform برای محاسبه ی مقادیر پیکسل های خروجی، از درون یابی استفاده می کند.
گام شماره 5: مشاهده ی عکس خروجی
پس از اینکه تبدیل مورد نظر انجام شد، ممکن است شما بخواهید عکس تبدیل شده را مشاهده کنید. مثال زیر از تابع imshow برای نمایش دادن عکس تبدیل شده، استفاده می کند:
مثال (تبدیلات فضایی دو بعدی اصلی در متلب)
figure, imshow(cb_trans)

درک چگونگی نمایش یافتن عکس تبدیل شده
هنگامی که به عکس تبدیل شده نگاهی بیاندازیم، مخصوصا در عملیات انتقال، ظاهراً به نظر می رسد که هیچ اتفاقی رخ نداده است. و عکس تبدیل شده با عکس اصلی یکسان به نظر می رسد. اما اگر شما مقادیر xdata و ydata که توسط تابع imtransform برگردانده شده اند، را بررسی کنید متوجه خواهید شد که مختصات عکس تغییر کرده اند. مثلا مختصات گوشه ی بالا و سمت چپ عکس ورودی از مقدار (1,1) به (41,41) تغییر کرده است. و مختصات گوشه ی پایین و سمت راست، از مقدار (80,80) به مقدار (120,120) تغییر یافته است. درواقع مقدار 40 به هریک از نقاط اضافه شده است.
مثال (تبدیلات فضایی دو بعدی اصلی در متلب)
دلیل اینکه هیچ تغییری در خروجی مشاهده نمی شود این است که تابع imtransform عکس خروجی را اندازه بندی می کند تا تنها حاوی عکس تبدیل شده باشد نه اینکه حاوی تمام سیستم مختصات خروجی باشد. برای مشاهده ی تاثیر انتقال مورد نظر نسبت به عکس اصلی، شما می توانید از چند پارامتر اختیاری برای مشخص کردن سایز عکس خروجی استفاده کنید. همچنین می توانید مشخص کنید که چقدر از فضای خروجی در عکس خروجی اضافه شود.
مثال زیر، از دو پارامتر اختیاری XData و YData برای مشخص کردن میزان اضافه شدن فضای مختصات به عکس خروجی، استفاده می کند.
مثال (تبدیلات فضایی دو بعدی اصلی در متلب)
cb_trans2 = imtransform(cb, tform_translate,...
'XData',[1 (size(cb,2)+xform(3,1))],...
'YData', [1 (size(cb,1)+xform(3,2))]);
figure, imshow(cb_trans2)
نکته: همان طور که در عکس زیر مشاهده می کنید، تمام پیکسل های عکس خروجی که نشان دهنده ی موقعیت عکس خروجی در صفحه مختصات هستند، به رنگ سیاه نمایش داده می شوند. تابع imtransform یک مقدار به نام fill value را به این پیکسل ها اختصاص می دهد. این مثال از یک مقدار پیش فرض برای fill value استفاده می کند اما شما می توانید آن را به دلخواه خود تغییر دهید.

تعریف داده های تبدیلات فضایی
قبل از اینکه بتوانید یک تبدیل فضایی انجام دهید، ابتدا باید پارامترهای این تبدیل را تعریف کنید. در بخش های زیر، دو راه را برای تعریف تبدیلات فضایی نشان داده شده است که عبارتند از:
- استفاده از یک ماتریس تبدیل
- استفاده از مجموعه نقاط
با استفاده از هریک از این روش ها، درواقع شما نتیجه ی حاصل شده را به تابع maketform می دهید تا ساختار TFORM مورد نیاز برای تابع imtransform ایجاد شود.
استفاده از یک ماتریس تبدیل:
تابع maketform می تواند ماتریس های تبدیل گوناگونی را بپذیرد. سایز این ماتریس ها می تواند برای تبدیلات n -بعدی متفاوت باشد. اما چون تابع imtransform تنها تبدیلات 2-بعدی را انجام می دهد، شما تنها می توانید ماتریس های 3در3 را برای آن مشخص کنید. بعنوان مثال برای انجام تبدیلات از نوع آفین، می توانید از یک ماتریس 3×3 استفاده کنید. برای تبدیلات از نوع آفین(affine)، ستون آخر ماتریس ما باید حاوی 0 و 0 و 1 باشد. شما همچنین می توانید به جای این کار، یک ماتریس 3در2 را مشخص کنید؛ در این صورت تابع imtransform به طور اتوماتیک ستون سوم را اضافه می کند.
جدول زیر، لیست انواع تبدیلات آفین که می توانید با تابع imtransform انجام دهید را نشان می دهد. همچنین ماتریس تبدیل بکار رفته برای تعریف آن تبدیلات را نیز نشان می دهد. شما همچنین می توانید چند تبدیل آفین را در داخل یک ماتریس تعبیه کنید.
| تبدیل آفین | مثال | ماتریس تبدیل | توضیحات |
| انتقال(Translation) | 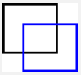 | 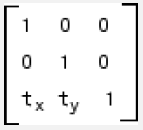 | \({ t }_{ x }\) میزان جابه جایی در طول محور x را مشخص می کند. \({ t }_{ y }\) میزان جابه جایی در طول محور y را مشخص می کند. |
| مقیاس(Scale) | 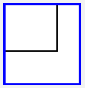 | 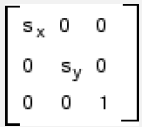 | \({ s }_{ x }\) ضریب مقیاس در طول محور x را مشخص می کند. \({ s }_{ y }\) ضریب مقیاس در طول محور y را مشخص می کند. |
| برش(انحراف) یا (Shear) |  |  | \({ sh }_{ x }\) ضریب انحراف در طول محور x را مشخص می کند. \({ sh }_{ y }\) ضریب انحراف در طول محور y را مشخص می کند. |
| چرخش(Rotation) |  |  | q زاویه ی چرخش را مشخص می کند. |
استفاده از مجموعه نقاط:
به جای مشخص کردن یک ماتریس تبدیل، می توانید از یک مجموعه از نقاط برای مشخص کردن تبدیلات استفاده کنید و به تابع maketform امکان دهید تا ماتریس تبدیل را ایجاد کند. برای انجام این کار در یک تبدیل آفین، باید سه نقطه که در یک خط واقع نشده باشند را درعکس ورودی و در عکس خروجی انتخاب کنید. اما برای انجام یک تبدیل تصویری(projective) باید چهار نقطه را مشخص کنید.
در مثال زیر، سه نقطه به تابع maketform داده می شود و به این تابع اجازه می دهیم تا ماتریس تبدیل را ایجاد کند. این سه نقطه، درواقع سه گوشه ی عکس شطرنجی را در تصویر ورودی و خروجی مشخص می کنند.
مثال
in_points = [11 11;21 11; 21 21]
out_points = [51 51;61 51;61 61]
tform2 = maketform('affine',inpts,outpts)
پس از تعریف داده های تبدیلات که در موارد بالا به آن پرداخته شد، باید یک ساختار TFORM را ایجاد کنیم تا تبدیلات فضایی را مشخص کند. برای ایجاد یک ساختار TFORM می توانید از تابع maketform استفاده کنید. سپس باید این ساختار TFORM را به تابع imtransform بدهید تا تبدیلات را انجام دهد. شما همچنین می توانید با استفاده از تابع cp2tform یک TFORM را ایجاد کنید.
مثال زیر، یک ساختار TFORM ایجاد می کند که پارامترهای ضروری برای انجام یک انتقال را مشخص می کند:
مثال
tform_translate = maketform('affine',xform) برای ایجاد یک TFORM ابتدا باید نوع تبدیلی که می خواهیم انجام دهیم را مشخص کنیم و سپس آن را به تابع maketform بدهیم. همان طور که در مثال بالا مشاهده می کنید، مقدار affine بعنوان نوع تبدیلات مشخص شده است. اما تابع maketform قادر است تا تبدیلات تصویری(projective) را نیز انجام دهد و از آن پشتیبانی می کند. جدول زیر لیست انواع تبدیلاتی را نشان می دهد که تابع maketform از آنها پشتیبانی می کند:
| نوع تبدیلات | توضیحات |
| 'affine' | به تبدیلاتی از قبیل انتقال، چرخش، مقیاس، و برش گفته می شود. در این نوع تبدیل، خطوط مستقیم، مستقیم می مانند و خطوط موازی نیز موازی می مانند اما مستطیل ها ممکن است به متوای الاضلاع تبدیل شوند. |
| 'projective' | به تبدیلاتی گفته می شود که در آن، خطوط مستقیم، مستقیم باقی می مانند اما خطوط موازی به سمت نقاط گریز(محو) همگرا می شوند. |
| 'box' | یک نوع خاص از تبدیلات آفین است، به طوری که ابعاد آن تغییر کرده و بطور مستقل مقیاس دهی شده است. |
| 'custom' | یک نوع تبدیل است که توسط کاربر تعریف شده است. |
| 'composite' | ترکیبی از دو یا چند تبدیل است. |