نکته: تبدیل فوریه بر روی یک تابع اعمال می شود تا یک تابع جدید تولید شود.
تبدیل فوریه بر روی تابع پیوسته ی \(f\left( t \right) \) که دارای یک متغیر پیوسته می باشد، با نماد 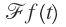 نشان داده می شود و با معادله ی زیر بیان می شود:
نشان داده می شود و با معادله ی زیر بیان می شود:
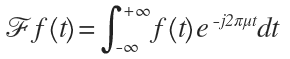
(معادله ی 4.2.15)
به طوری که \(\mu \) نیز یک متغیر پیوسته است. به دلیل اینکه از t انتگرال گیری می شود، 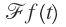 تنها تابعی از \(\mu \) است. این حقیقت را به صورت
تنها تابعی از \(\mu \) است. این حقیقت را به صورت 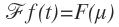 می نویسیم. بنابراین برای راحتی، تبدیل فوریه ی \(f\left( t \right) \) را به صورت زیر می نویسیم:
می نویسیم. بنابراین برای راحتی، تبدیل فوریه ی \(f\left( t \right) \) را به صورت زیر می نویسیم:
$$F(\mu )=\int _{ -\infty }^{ +\infty }{ f\left( t \right) { e }^{ -j2\pi \mu t }dt } $$
(معادله ی 4.2.16)
به طور برعکس، اگر \(F(\mu )\) داده شده باشد، می توانیم \(f(t)\) را به دست بیاوریم. این کار را با استفاده از تبدیل معکوس فوریه انجام می دهیم که با نماد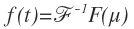 نشان داده می شد به صورت زیر بیان می شود:
نشان داده می شد به صورت زیر بیان می شود:
$$f(t)=\int _{ -\infty }^{ +\infty }{ F(\mu ){ e }^{ j2\pi \mu t }d\mu } $$
(معادله ی 4.2.17)
به دلیل اینکه از متغیر \(\mu \) در تبدیل معکوس فوریه انتگرال گیری می شود، معادله ی بالا تنها تابعی از t است. بنابراین به جای استفاده از نمادهای گیج کننده، تنها آن را به صورت \(f\left( t \right) \) می نویسیم یعنی:
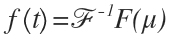
به معادلات 4.2.16 و 4.2.17 معمولا جفت معادلات تبدیل فوریه گفته می شود. این معادلات بیان می کنند که می توان یک تابع را از تبدیل آن، بازیابی کرد.
با استفاده از فرمول اویلر، می توانیم معادله ی 4.2.16 را به صورت زیر بنویسیم:
$$F(\mu )=\int _{ -\infty }^{ +\infty }{ f(t)\left[ \cos { (2\pi \mu t) } -j\sin { (2\pi \mu t) } \right] } dt$$
(معادله ی 4.2.18)
اگر \(f(t)\) حقیقی باشد، به طور کلی مشاهده می کنیم که تبدیل آن، مختلط است.
توجه کنید که تبدیل فوریه یک بسط از \(f(t)\) است که در جملات سینوسی (و کسینوسی) ضرب شده است به طوری که فرکانس آنها با استفاده از مقادیر \(\mu \) تعیین می شود. (زیرا همان طور که قبلا گفته شد، از متغیر t انتگرال گیری می شود).
به دلیل اینکه تنها متغیر باقی مانده پس از انتگرال گیری، فرکانس است، به دامنه ی آن، دامنه یا حوزه ی فرکانس(frequency domain) گفته می شود.
بعدا در این فصل، به طور مفصل در مورد حوزه ی فرکانس و ویژگی های آن بحث خواهیم نمود.
در بحث بالا، متغیر t می تواند هر نوع متغیر پیوسته ای باشد. و احدهای متغیر فرکانس یعنی \(\mu\) به واحدهای t بستگی دارد. بعنوان مثال، اگر متغیر t زمان را در واحد ثانیه مشخص کند، واحد \(\mu\) سیکل بر ثانیه یا همان هرتز(Hz) خواهد بود. اگر t فاصله را به متر مشخص کند، آنگاه واحد \(\mu\) سیکل بر متر خواهد بود. و همین طور الی اخر.
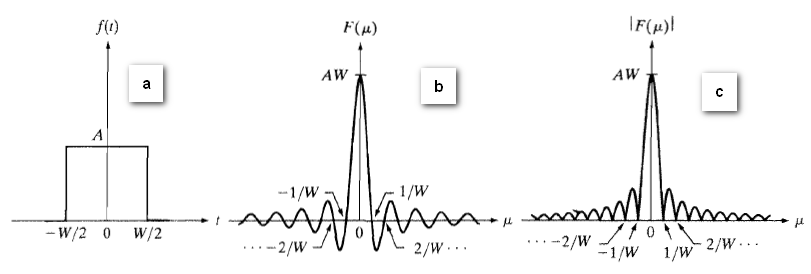 (عکس 4.4)
(عکس 4.4)
تبدیل فوریه تابع a در تصویر بالا، از معادله ی 4.2.16 به صورت زیر استنباط می شود:
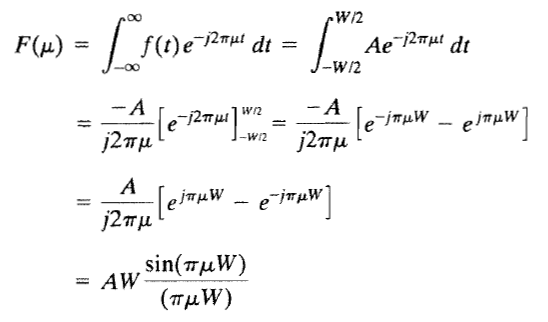
به طوری که در آن از معادله ی مثلثاتی \(\sin { \theta =({ e }^{ j\theta }-{ e }^{ -j\theta })/2j } \) استفاده کردیم. بنابراین در این مثال، جملات مختلط تبدیل فوریه به خوبی با توابع سینوسی جایگزین شدند.
به نتیجه ی به دست آمده در مثال بالا، تابع sinc گفته می شود:
$$sinc(m)=\frac { \sin { (\pi m) } }{ \pi m } $$
ص 229




