
همان طور که در تصویر بالا مشاهده می کنید، در این سری از مقالات، به ترجمه ی کتاب electronics fundamentals می پردازیم. این کتاب را می توان یکی از بهترین منابع برای آموزش مبانی الکترونیک دانست. در این کتاب بطور ساده مفاهیم مختلف آموزش داده شده است و همچنین در ترجمه سعی شده است تا سادگی بیان رعایت شود.
در میدان های الکتریکی و الکترونیکی، با مقادیر بسیار کوچک و بسیار بزرگ، مواجه خواهید شد. بعنوان مثال، جریان الکتریکی درقطعات برق قدرت می تواند از هزاران آمپر فراتر رود و یا در مدارهای الکتریکی می تواند کوچکتر از یک هزارم یا یک میلیونیم آمپر باشد. این تغییرات مقادیر ذکر شده، تنها نمونه ای از دیگر مقادیر الکتریکی است. نمادگذاری مهندسی درواقع یک نوع خاص از نمادگذاری علمی است. از این نوع نمادگذاری به طور گسترده، در زمینه های فنی برای بیان مقادیر بزرگ و کوچک استفاده می شود.
در الکترونیک، از نمادگذاری مهندسی برای بیان مقادیری همچون ولتاژ، جریان، توان، مقاومت و دیگر کمیت ها استفاده می شود. پس از تکمیل این بخش، شما قادر خواهید بود کارهای زیر را انجام دهید:
- استفاده از نماد علمی برای نمایش دادن مقادیر
- بیان کردن تمامی اعداد با استفاده از توان های عدد 10
- انجام محاسبات با استفاده از توان های عدد 10
نمادگذای علمی، یک روش مناسب برای بیان اعداد بزرگ و اعداد کوچک است. از این نوع نمادگذاری برای انجام محاسبات بر روی چنین اعدادی استفاده می شود. در نمادگذاری علمی، یک رقم از مقدار مورد نظر در سمت چپ از نقطه ی اعشار قرار می گیرد و سپس در توان هایی از عدد 10 ضرب می شود. بعنوان مثال مقدار 150000 در نمادگذاری علمی بصورت \(1.5\times { 10 }^{ 5 }\) بیان می شود و مقدار 0.00022 به صورت \(2.2\times { 10 }^{ -4 }\) بیان می شود.
توان های عدد 10
در جدول 1، برخی از توان های مثبت یا منفی عدد 10 را به همراه اعداد متناسب با آنها مشاهده می نمایید. در هر یک از این موارد، اعداد به صورت توانی از 10 (در مبنای عدد 10) نشان داده شده است. یک توان، عددی است که مبنا به تعداد آن، در خودش ضرب می شود. توان، مشخص می کند که برای ایجاد یک عدد، نقطه ی اعشار باید چه مقدار به سمت راست یا چپ حرکت کند. برای به دست آوردن یک توان مثبت از عدد 10، نقطه ی اعشار را به اندازه ی آن توان به سمت راست ببرید. و یا به عبارت دیگر، به اندازه ی آن توان، در جلوی عدد 1، صفر قرار دهید. بعنوان مثال برای توان 4 داریم:
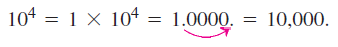
جدول شماره 1
برخی از توان های مثبت و منفی عدد 10 را نشان می دهد.
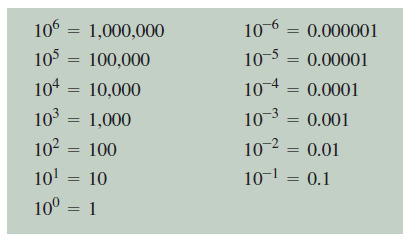
برای توان های منفی عدد 10، نقطه ی اعشار را به اندازه ی توان، به سمت چپ ببرید. بعنوان مثال برای توان 4- از عدد 10 به صورت زیر عمل می کنیم:
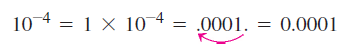
مثال شماره 1
هر یک از اعداد زیر را با استفاده از نماد علمی بیان کنید:
1) 240 2) 5100 3) 85000 4) 3350000
راه حل: در هریک از موارد، نقطه ی اعشار را به سمت چپ ببرید و سپس به تعداد رقم هایی که نقطه اعشار به سمت چپ رفته است، نتیجه را در توان مثبت 10 ضرب کنید. بصورت زیر:
1) \(240=2.4\times { 10 }^{ 2 }\)
2) \(5100=5.1\times { 10 }^{ 3 }\)
3) \(85000=8.5\times { 10 }^{ 4 }\)
4) \(3350000=3.35\times { 10 }^{ 6 }\)
مسأله: عدد 750000000 را با نماد علمی بیان کنید.
مثال شماره 2
هریک از اعداد زیر را با استفاده از نماد علمی بیان کنید:
1) 0.24 2) 0.005 3) 0.00063 4) 0.000015
راه حل: در هریک از موارد، نقطه ی اعشار را به سمت راست ببرید و سپس به تعداد رقم هایی که نقطه ی اعشار به سمت راست رفته است، نتیجه را در توان منفی عدد 10 ضرب کنید:
1) \(0.24=2.4\times { 10 }^{ -1 }\)
2) \(0.005=5\times { 10 }^{ -3 }\)
3) \(0.00063=6.3\times { 10 }^{ -4 }\)
4) \(0.000015=1.5\times { 10 }^{ -5 }\)
مسأله: عدد 0.00000093 را با استفاده از نماد علمی، بیان کنید.
مثال شماره 3
هریک از اعداد زیر را به اعداد معمولی(شمارشی) تبدیل کنید:
1) \(1\times { 10 }^{ 5 }\)
2) \(2.9\times { 10 }^{ 3 }\)
3) \(3.4\times { 10 }^{ -2 }\)
4) \(2.5\times { 10 }^{ -6 }\)
راه حل: با توجه به مثبت یا منفی بودن توان، نقطه ی اعشار را به سمت راست یا چپ ببرید. بصورت زیر:
1) \(1\times { 10 }^{ 5 }=100,000\)
2) \(2.9\times { 10 }^{ 3 }=2900\)
3) \(3.2\times { 10 }^{ -2 }=0.032\)
4) \(2.5\times { 10 }^{ -6 }=0.0000025\)
مسأله: عدد \(8.2\times { 10 }^{ 8 }\) را بصورت یک عدد معمولی(شمارشی) بیان کنید.






