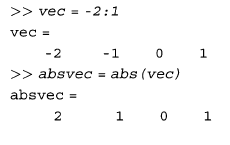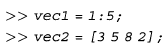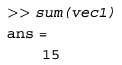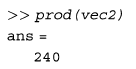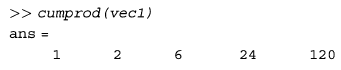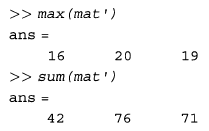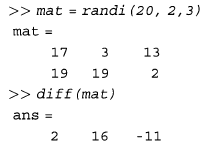در متلب، یک بردار یا یک ماتریس را می توان بعنوان آرگومان به یک تابع داد. سپس این تابع می تواند بر روی هر عنصر از این ماتریس یا بردار، عملیاتی را انجام دهد. این بدین معنی است که آنچه در خروجی به دست می آوریم، سایزی همچون سایز آرگومان ورودی خواهد داشت.
بعنوان مثال، اجازه دهید تا قدر مطلق هریک از عناصر بردار vec را به دست بیاوریم. تابع abs به طور اتوماتیک قدر مطلق تک تک عناصر بردار ما را محاسبه کرده و خروجی ما یک بردار با همان طول قبلی خواهد بود. (یعنی طول این بردار تغییری نمی کند). به مثال زیر توجه کنید:
مثال (بردارها و ماتریس ها بصورت آرگومان توابع)
اما اگر از یک ماتریس بعنوان آرگومان ورودی استفاده کنیم، ماتریس به دست آمده اندازه ای یکسان با آن خواهد شد. بعنوان مثال تابع sign، علامت هریک از عناصر یک ماتریس را مشخص می کند:
مثال (بردارها و ماتریس ها بصورت آرگومان توابع)
توابعی مثل abs و sign می توانند هر عدد یا بردار یا ماتریسی را بپذیرند. توابع زیادی وجود دارند که مخصوص انجام عملیات بر روی بردارها یا ستون های ماتریس ها هستند. بعنوان نمونه می توان توابع min و max و sum و prod را نام برد. ابتدا این توابع را بر روی بردارها و سپس بر روی ماتریس ها بکار می بریم.
بعنوان مثال فرض کنید که مغیرهای برداری زیر را داریم:
مثال (بردارها و ماتریس ها بصورت آرگومان توابع)
تابع min در متلب، مینیمم مقدار یک بردار را برمی گرداند و تابع max ماکسیمم مقدار یک بردار را برمی گرداند:
مثال (بردارها و ماتریس ها بصورت آرگومان توابع)
تابع sum تمام درایه های یک بردار را با یکدیگر جمع می کند. بعنوان مثال اگر بردار vec1 را به این تابع بدهیم، مقدار 5+4+3+2+1 یا 15 بازگردانده می شود:
مثال (بردارها و ماتریس ها بصورت آرگومان توابع)
تابع prod حاصلضرب تمام درایه های درون یک بردار را برمی گرداند. بعنوان مثال بردار t2 مقدار 2*8*5*3 یعنی 240 را برمی گرداند:
مثال (بردارها و ماتریس ها بصورت آرگومان توابع)
همچنین توابعی وجود دارند که مجموع بازگشتی را محاسبه می کنند.
توابع cumsum و cumprod درواقع جمع بازگشتی و ضرب بازگشتی را مورد محاسبه قرار می دهند. بعنوان مثال در بردار vec1 ، جمله ی اول جمع بازگشتی برابر است با 1، جمله ی دوم برابر است با 3 (2+1)، جمله ی سوم برابر است با 6(3+2+1) و جمله ی چهارم برابر است با 10(4+3+2+1) و جمله ی آخر برابر است با 15(5+4+3+2+1).
خروجی ما یک بردار خواهد بود که به تعداد بردار اولیه ی ما، درایه دارد:
مثال (بردارها و ماتریس ها بصورت آرگومان توابع)
تابع cumprod ضرب بازگشتی عناصر را مورد محاسبه قرار داده و نتیجه را بصورت یک بردار هم اندازه با بردار اولیه، ذخیره می کند:
مثال (بردارها و ماتریس ها بصورت آرگومان توابع)
همچنین به طور مشابه، توابعی به نام cummin و cummax وجود دارند که در متلب ورژن R2014b معرفی شده اند. همچنین در این ورژن از متلب، یک گزینه به نام 'reverse' برای تمام توابع بازگشتی معرفی شده است. بعنوان مثال داریم:
مثال (بردارها و ماتریس ها بصورت آرگومان توابع)
در ماتریس ها، تمامی این توابع بر روی هر ستون منحصر به فرد اجرا می شوند. اگر یک ماتریس دارای ابعاد r×c باشد، نتیجه ی به دست آمده برای توابع min و max و sum و prod بصورت یک بردار با ابعاد \(1\times c\) خواهد بود که به ترتیب، مینیمم و ماکزیمم و جمع و ضرب را برای هر ستون محاسبه می کنند. بعنوان مثال ماتریس زیر را در نظر بگیرید:
مثال (بردارها و ماتریس ها بصورت آرگومان توابع)
در زیر، مقدار توابع maxو sum برای این ماتریس را محاسبه کرده ایم:
مثال (بردارها و ماتریس ها بصورت آرگومان توابع)
برای اینکه بتوانید یکی از این توابع را بر روی هر سطر از ماتریس مورد نظر اعمال کنید، می توانید از روش زیر استفاده کنید(ایجاد ترانهاده):
مثال (بردارها و ماتریس ها بصورت آرگومان توابع)
سوال سریع!
با توجه به اینکه این توابع به صورت ستونی عمل می کنند، چگونه می توانیم مقدار ماکسیمم یک ماتریس را پیدا کنیم؟
پاسخ: ابتدا ما با استفاده از دستور max بزرگترین عدد در بین ستون ها را محاسبه می کنیم. و سپس دوباره از تابع max استفاده می کنیم تا از اعداد به دست آمده، مقدار ماکسیمم را محاسبه کنیم. به عبارت دیگر، به طور تو در تو از دستور max استفاده می کنیم. مثال:
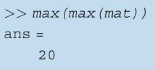
توابع cumsum و cumprod نیز جمع یا ضرب هر ستون را بصورت بازگشتی محاسبه می کنند. ماتریس به دست آمده دارای همان ابعاد قبلی را دارا است:
مثال (بردارها و ماتریس ها بصورت آرگومان توابع)
توجه کنید که اولین سطر در ماتریس حاصل شده ی بالا، مشابه با اولین سطر از ماتریس ورودی است. پس از این سطر، مقادیر درون سطرها روی یکدیگر انباشته می شوند. به طور مشابه، توابع cummin و cummax مینیمم بازگشتی و ماکسیمم بازگشتی را مورد محاسبه قرار می دهند:
مثال (بردارها و ماتریس ها بصورت آرگومان توابع)
یک تابع کاربردی دیگر که می تواند همراه بردارها و ماتریس ها به کار رود، تابع diff است. تابع diff اختلافات متوالی درایه های یک بردار را برمی گرداند. بعنوان مثال داریم:
مثال (بردارها و ماتریس ها بصورت آرگومان توابع)
اگر یک بردار به نام v داشته باشیم، که طول آن n باشد، طول \(diff(v)\) برابر با \(n-1\) خواهد بود. در یک ماتریس، تابع diff بر روی هر ستون اعمال می شود:
مثال (بردارها و ماتریس ها بصورت آرگومان توابع)