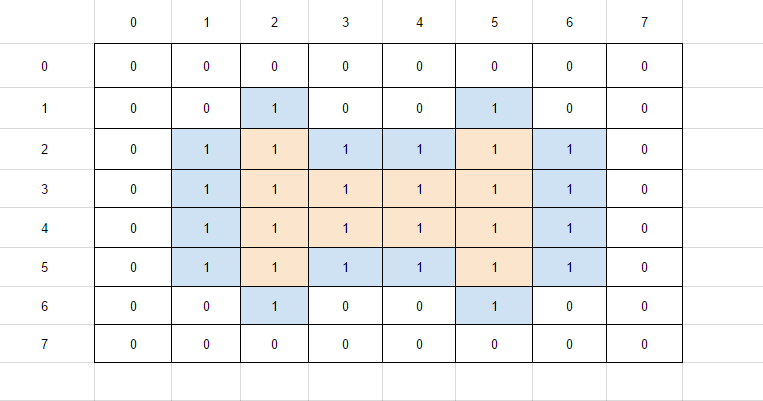
اگر مجموعه های A و B زیرمجموعه ای از \({ z }^{ 2 }\) باشند، آنگاه دایلیشن باینری مجموعه ی A توسط B، با نماد \(A{ \oplus }_{ b }B\) نشان داده می شود و به صورت زیر تعریف می شود:
$$A{ \oplus }_{ b }B=\{ c\in { Z }^{ 2 }|c=a+b\quad for\quad some\quad a\in A\quad ,\quad b\in B\} $$
نکته: در دایلیشن،حرف زیر نویس b کوچک، به معنی باینری(binary) است.
و یا به عبارت دیگر، می توانیم دایلیشن را بصورت زیر تعریف کنیم:
$$A{ \oplus }_{ b }B=\bigcup _{ b\in B }^{ }{ { (A) }_{ b }= } \bigcup _{ a\in A }^{ }{ { (B) }_{ a } } $$
به مثال زیر توجه کنید:

با تماشای ویدیوی زیر، بهتر می توانید مفهوم دایلیشن را متوجه شوید:
اکنون به یک مثال واضح تر توجه کنید:
فرض کنید عکسی به نام A به صورت زیر داریم:
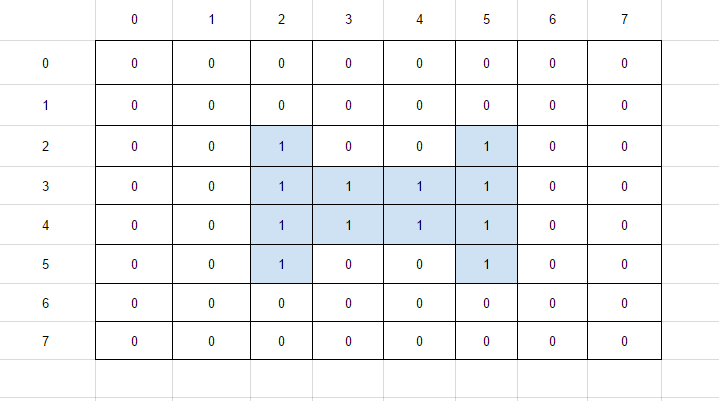
و یک عنصر ساختاری، به نام S به صورت زیر داریم به طوری که مبدا آن وسط این شکل است:
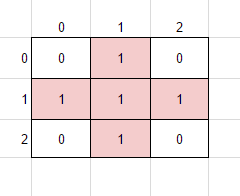
حالا A دایلیشن S به صورت زیر خواهد بود: