عملیات مجموعه ای بر روی تصاویر باینری

در مورفولوژی ریاضی، یک عکس به صورت یک مجموعه از بردارهای مختصات، در فضای اقلیدسی تعریف می شود. فرض کنیم که \({ E }^{ N }\) مجموعه ای از تمام نقاط به صورت \(p=({ x }_{ 1 },{ x }_{ 2 },...,{ x }_{ n })\) باشد که در فضای N بُعدی اقلیدسی تعریف شده اند. 

 حالا هر مجموعه ی A، متناظر است با یک عکس باینری. هر عکس باینری، یک ترکیب N-بعدی از رنگ های سیاه و سفید است. به طوری که نقطه ی p در عکس باینری ما به رنگ سیاه است اگر و تنها اگر \(p\in A\) باشد، در غیر این صورت p سفید است. 

یک عکس باینری در مجموعه ی \({ E }^{ 2 }\) یک سایه ی سیاه رنگ است. یا به عبارت دیگر مجموعه ای از پیکسل های سیاه رنگ است. یک عکس باینری در فضای \({ E }^{ 3 }\)  یک جسم است. یا به عبارت دیگر، مجموعه ای از محیط و ناحیه های درونی اشیاء است. 

مفهوم یک عکس باینری، با مفهوم پیکسل های سیاه و سفید در سیستم مختصات دکارتی ارتباط دارد. 

 فرض کنیم که A، یک مجموعه (یا عکس باینری) در فضای \({ E }^{ 2 }\) باشد. در صورتی که یک مجموعه حاوی هیچ عضوی نباشد، به آن یک مجموعه ی تهی گفته می شود. یا به عبارت دیگر با علامت \(\phi  \) نشان داده می شود. 

 فرض کنیم که \(a\in A\) یک عنصر به صورت \(a=({ a }_{ 1 },{ a }_{ 2 })\) در مجموعه ی A باشد. در این صورت متمم عکس A، یک عکس باینری دیگر است که عناصر سیاه و سفید آنها معکوس شده باشند( یعنی 1ها بشوند 0 و صفرها بشوند 1). 

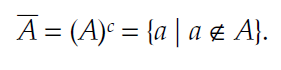
متمم A، یا A به توان c، برابر است با a ها به طوری که آن a ها عضو A نباشند. 

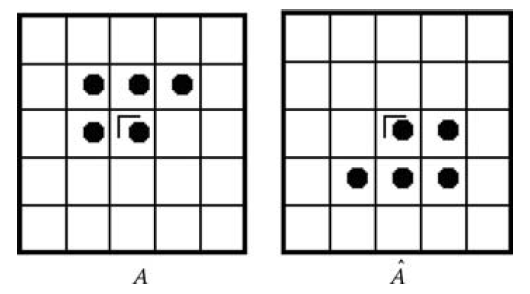
اگر یک عکس به نام A داشته باشیم، آنگاه منظور از انعکاس عکس A، انعکاس آن نسبت به مبدا می باشد. و به صورت زیر تعریف می شود:

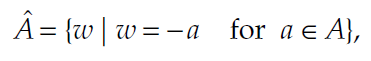
 به طوری که در آن، عناصر به صورت \(({ a }_{ 1 },{ a }_{ 2 })\) منفی(قرینه)  شده اند.  یک مثال از انعکاس، در عکس ۲.۱ نشان داده شده است. به طوری که مبدا مختصات در پیکسل وسطی قرار دارد. 

اجتماع دو عکس a و b ، یک عکس باینری است که در آن داریم: اگر یک پیکسل در A یا B سیاه باشد، آنگاه در اجتماع این دو، آن پیکسل سیاه خواهد بود.  به مجموعه ی زیر دقت کنید:

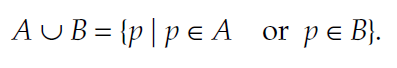
اشتراک دو عکس a و b یک عکس باینری است به طوری که : اگر یک پیکسل در هر دوی مجموعه های a و b سیاه باشد، این پیکسل در اشتراک این دو مجموعه نیز سیاه خواهد بود. به مجموعه ی زیر دقت کنید: 

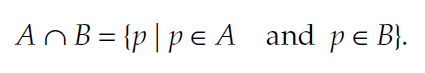
با استفاده از قوانین دمورگان، می توان اجتماع را به اشتراک و یا اشتراک را به اجتماع تبدیل نمود. به قوانین زیر توجه کنید:

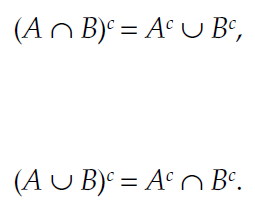
تفاضل دو مجموعه ی A و B ، بصورت A-B یا A\B نشان داده می شود. که به معنای پیکسل های درون مجموعه A است که در مجموعه ی B وجود ندارند. می توانیم تفاضل دو مجموعه را بصورت زیر بیان کنیم: 

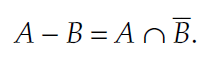
تعداد اعضای مجموعه ی A ، یا تعداد عناصر مجموعه ی A ، به صورت های A# یا |A| نمایش داده می شود. و یا به صورت (Card(A نشان داده می شود.بعنوان مثال،  اگر مجموعه ی A ، تعداد n عضو (عنصر) متمایز از اعداد طبیعی داشته باشد، تعداد اعضای مجموعه ی A برابر با n است. 

• قبلی