مقدمه ای در مورد سری و تبدیل فوریه

جوزف فوریه، یک ریاضی دان فرانسوی بود که در سال 1768 در شهر Auxerre به دنیا آمد. 

علت ماندن این ریاضی دان در خاطره ها، انتشار کتابی به نام نظریه ی تحلیلی گرما است که در سال 1822 منتشر شد. 

فوریه در این زمینه می گوید که، هر تابع متناوب می تواند به صورت جمع توابع سینوس و یا کسینوس با فرکانس های متفاوت تعریف شود به طوری که هرکدام از آنها در یک ضریب متفاوت ضرب شده باشند. به این جمع، سری فوریه می گوییم. 

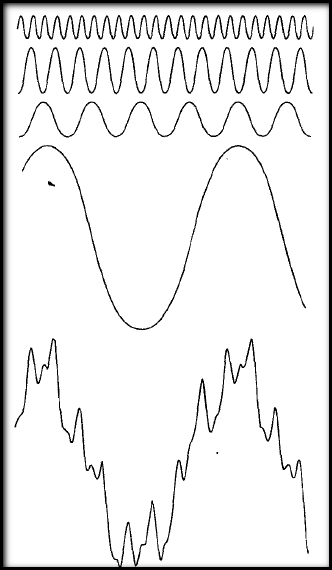
(در تصویر بالا، پایین ترین تابع، از جمع چهار تابع بالای آن به دست می آید. )

 مفاهیم اولیه در تبدیل فوریه

اعداد مختلط

 عدد مختلط C به صورت زیر تعریف می شود: 

$$C=R+jI$$

 به طوری که R و I اعدادی حقیقی هستند و j یک عدد موهومی است که برابر با جذر 1- است. بنابراین \(j=\sqrt { -1 } \) . در اینجا، به R، جزء حقیقی این عدد مختلط گفته می شود و به I جزء موهومی گفته می شود. 

اعداد حقیقی زیرمجموعه ی اعداد مختلط هستند به طوری که در اعداد حقیقی \(I=0\) است. 

 مزدوج عدد مختلط C را با نماد \({ C }^{ * }\) نشان می دهیم و به صورت زیر تعریف می کنیم: 

$${ C }^{ * }=R-jI$$

تعبیر هندسی اعداد مختلط

 اعداد مختلط را می توان به صورت نقاطی در صفحه ی مختصات در نظر گرفت که به آن صفحه ی مختلط گفته می شود. به طوری که به محور افقی، محور حقیقی می گوییم و مقادیر R را بر روی آن مشخص می کنیم. و به محور عمودی، محور موهومی می گوییم که مقادیر I را بر روی آن مشخص می کنیم. بنابراین عدد مختلط \(R+jI\) را به صورت نقطه ی \((R,I)\) در سیستم مختصات صفحه ی مختلط نشان می دهیم. 

بعضی مواقع بهتر است که اعداد مختلط را در مختصات قطبی نشان دهیم: 

$$C=\left| C \right| (\sin { \theta  } +j\cos { \theta  } )$$

 به طوری که \(\left| C \right| =\sqrt { { R }^{ 2 }+{ I }^{ 2 } } \) طول بردار کشیده شده از مبدا صفحه ی مختلط به نقطه ی \((R,I)\) است و \(\theta \) نیز زاویه ی بین این بردار و محور حقیقی است. 

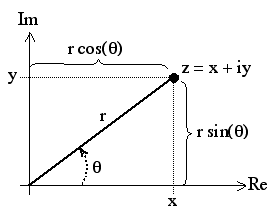
 با کمک گرفتن از نمودار بالا، متوجه می شویم که \(\tan { \theta  } =\frac { I }{ R } \) یا \(\quad \theta =\arctan { (\frac { I }{ R } ) } \) . تابع arctan مذکور، زاویه ها را در بازه ی بسته ی \([\frac { -\pi  }{ 2 } ,\frac { \pi  }{ 2 } ]\) برمی گرداند. 

اما به دلیل اینکه I و R می توانند مستقل از یکدیگر، مثبت یا منفی باشند، نیاز داریم که زاویه ها را در بازه ی بسته ی \([-\pi ,\pi ]\) به دست بیاوریم. 

برای انجام این کار، به سادگی می توانیم به هنگام محاسبه ی \(\theta \) علامت های I وR را مورد بررسی قرار دهیم. 

اکثر زبان های برنامه نویسی، این کار را به طور اتوماتیک انجام می دهند، بعنوان مثال، برای انجام این کار در متلب، می توانیم از فرمول \(atan2(Img,Real)\) استفاده کنیم. 

با استفاده از فرمول اویلر، که به صورت زیر تعریف می شود: 

$${ e }^{ j\theta  }=\cos { \theta +j\sin { \theta  }  } $$

 ;که در آن \(e=2.71828...\) است، می توانیم در مختصات قطبی، اعداد مخلط را به صورت زیر نشان دهیم: 

$$C=\left| C \right| { e }^{ j\theta  }$$

 به طوری که \(\left| C \right| \) و \(\theta \) در بالا تعریف شده اند. 

 بعنوان مثال، عدد مختلط \(1+2j\) در مختصات قطبی به صورت \(\sqrt { 3 } { e }^{ j\theta  }\) نشان داده می شود به طوری که \(\theta =64.4\) درجه یا به عبارت دیگر \(\theta \) برابر است با 1.1 رادیان. 

 معادلات قبلی، در توابع مختلط نیز کاربرد دارند. بعنوان مثال، یک تابع مختلط به نام \(F\left( u \right) \) که تابع متغیر u می باشد، می تواند بصورت حاصل جمع \(F\left( u \right) =R\left( u \right) +jI\left( u \right) \) بیان شود به طوری که \(R\left( u \right) \) و \(I\left( u \right) \) به ترتیب توابع جزء حقیقی و جزء موهومی هستند. 
همان طور که قبلا ذکر شد، مزدوج تابع \(F\left( u \right) \) با نماد \({ F }^{ * }\left( u \right) \) و به صورت \({ F }^{ * }\left( u \right) =R\left( u \right) -jI\left( u \right) \) نشان داده می شود. و اندازه ی آن برابر است با \(\left| F\left( u \right)  \right| =\sqrt { R{ (u) }^{ 2 }+I{ (u) }^{ 2 } } \). و زاویه ی آن برابر است با \(\theta \left( u \right) =\arctan { (\frac { I\left( u \right)  }{ R\left( u \right)  } ) } \). 

• قبلی
• بعدی