حل یک مسئله ی غیرخطی محدود در متلب

در این بخش با موارد زیر آشنا خواهید شد: 

1. تعریف مسئله: تابع روزن بروک
2. تعریف این مسئله در نرم افزار متلب
3. اجرای بهینه سازی در متلب
4. تفسیر نتایج به دست آمده در متلب

 تعریف مسئله: تابع روزن بروک

فرض کنید که می خواهیم حداقل تابع روزن بروک  که بصورت زیر تعریف می شود را پیدا کنیم:

$$f\left( x \right) =100{ ({ x }_{ 2 }-{ x }_{ 1 }^{ 2 }) }^{ 2 }+{ (1-{ x }_{ 1 }) }^{ 2 }$$

 به طوری که این تابع بر روی یک دایره با شعاع واحد تعریف شده باشد. بعنوان مثال یک دایره با شعاع 1 که در وسط مبدا قرار گرفته باشد. بعبارت دیگر می خواهیم کمترین مقدار تابع \(f\left( x \right) \) را پیدا کنیم به طوری که \({ x }_{ 1 }^{ 2 }+{ x }_{ 2 }^{ 2 }\le 1\)  . این یک مسئله در کمینه گیری از یک تابع غیرخطی با یک محدودیت غیرخطی می باشد. 

 نکته: تابع روزن بروک یک تابع تست استاندارد در بهینه سازی می باشد. مقدار مینیمم یکتای این تابع 0 است که در نقطه ی \((1,1)\) به دست می آید. 

در زیر دو نمودار از جهات مختلف تابع روزن بروک در دایره ی واحد نشان داده شده است. محور عمودی بصورت لگاریتمی مقیاس دهی شده است. بعبارت دیگر بصورت \(\log { (1+f\left( x \right) ) } \) ترسیم شده است. 

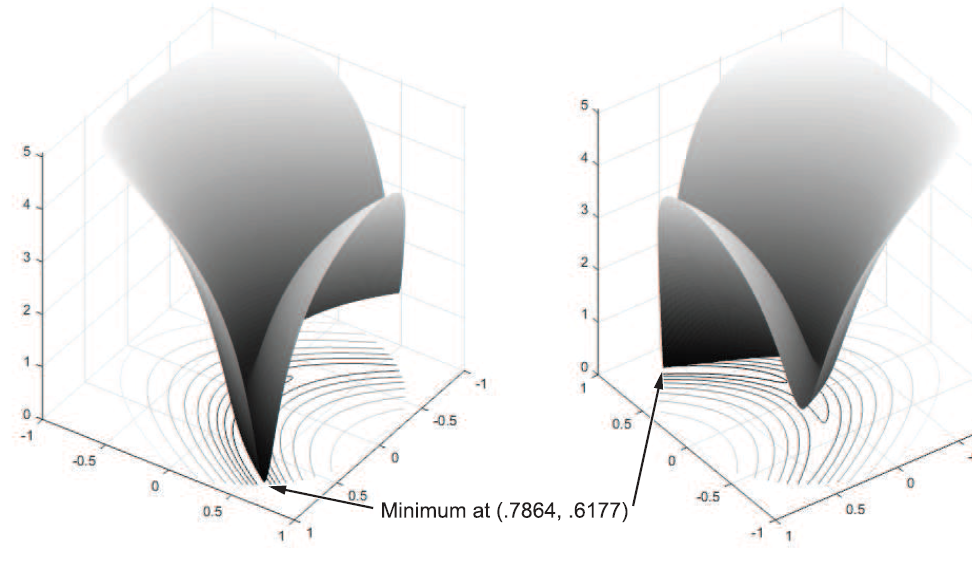
 به تابع \(f\left( x \right)\) تابع هدف(objective) گفته می شود. این همان تابعی است که می خواهیم کمینه ی آن را محاسبه کنیم. به نامعادله ی \({ x }_{ 1 }^{ 2 }+{ x }_{ 2 }^{ 2 }\le 1\) محدودیت(constraint) گفته می شود.  این محدودیت ها درواقع مجموعه ی x را که می خواهیم در آن به دنبال مینیمم بگردیم، محدود می کنند. شما می توانید هرتعداد محدودیت که بخواهید، داشته باشید، چه معادله باشند و چه نامعادله. تمام توابع بهینه سازی در جعبه ابزار متلب، تنها مینیمم توابع هدف را محاسبه می کنند. اما برای محاسبه ی بیشینه ی  تابع f می توانید مینیمم f- را مورد محاسبه قرار دهید. 

تعریف این مسئله در نرم افزار متلب

 به منظور استفاده از بهینه ساز جعبه ابزار متلب، نیاز داریم تا کارهای زیر را انجام دهیم:

1. ابتدا باید تابع مورد نظر(تابع هدف) را به زبان متلب بنویسید. یعنی به صورت یک m-فایل یا بصورت یک تابع بی نام. در این مثال از یک m-فایل استفاده خواهیم نمود.

2. باید محدودیت خودرا بصورت یک فایل مجزا و یا یک تابع بی نام تعریف نماییم. 

 این موارد به ترتیب در زیر توضیح داده شده اند.

ایجاد m-فایل برای تابع هدف

 m-فایل درواقع یک فایل متنی است که حاوی دستورات متلب می باشد و پسوند آن m. است. برای انجام این کار، می توانید از منوی بالای نرم افزار متلب، بر روی new کلیک کنید و سپس function را انتخاب کنید. و یا اینکه می توانید در ادیتور متلب به صورت زیر عمل کنید: 

1. در پنجره ی command در متلب دستور زیر را تایپ کنید و کلید Enter را فشار دهید: 

edit rosenbrock

 خواهید دید که ادیتور نرم افزار متلب باز خواهد شد. 

 2. حالا کدهای زیر را در داخل ادیتور باز شده کپی کنید: 

function f = rosenbrock(x)
f = 100*(x(2) - x(1)^2)^2 + (1 - x(1))^2;

 حالا بر روی دکمه ی save کلیک کنید. 

ایجاد m-فایل برای تابع محدودیت

 توابع محدودیت باید فرمول بندی شوند. بنابراین باید به صورت \(c\left( x \right) \le 0\) یا \(ceq\left( x \right) =0\) بیان شوند. بنابراین محدودیت \({ x }_{ 1 }^{ 2 }+{ x }_{ 2 }^{ 2 }\le 1\) باید بصورت \({ x }_{ 1 }^{ 2 }+{ x }_{ 2 }^{ 2 }-1\le 0\)  بیان شود تا سینتکس صحیحی داشته باشد. 

 علاوه بر موارد ذکر شده، توابع جعبه ابزار متلب که محدودیت های غیرخطی را می پذیرند، به هردو حالت محدودیت ها نیاز دارند. یعنی هم به حالت معادله ای و هم به حالت نامعادله ای محدودیت ها نیاز دارند. در این مثال، تنها یک محدودیت نامعادله ای وجود دارد، بنابراین ما باید یک آرایه ی خالی([]) را بعنوان تابع معادله ای محدودیت به تابع محدودیت پاس دهیم( بعنوان آرگومان ceq). با درنظر گرفتن این شرایط، ما در زیر یک m-فایل برای محدودیت غیرخطی خود می نویسیم: 

1. یک m-فایل به نام unitdisk.m ایجاد کنید به طوری که حاوی کدهای زیر باشد: 

function [c, ceq] = unitdisk(x)
c = x(1)^2 + x(2)^2 - 1;
ceq = [ ];

 حالا این فایل را با نام unitdisk.m ذخیره کنید. 

اجرای بهینه سازی در متلب

دو راه برای اجرای بهینه سازی وجود دارد که عبارتند از: 

1. استفاده از Optimization app

2. استفاده از دستورات خط فرمان 

این موارد به ترتیب، در زیر نشان داده شده اند.

 استفاده از Optimization app یا اپلیکیشن بهینه سازی در متلب

1. دستور optimtool را در خط فرمان متلب تایپ کنید و کلید Enter را فشار دهید تا اپلیکیشن بهینه سازی شروع به کار کند. 

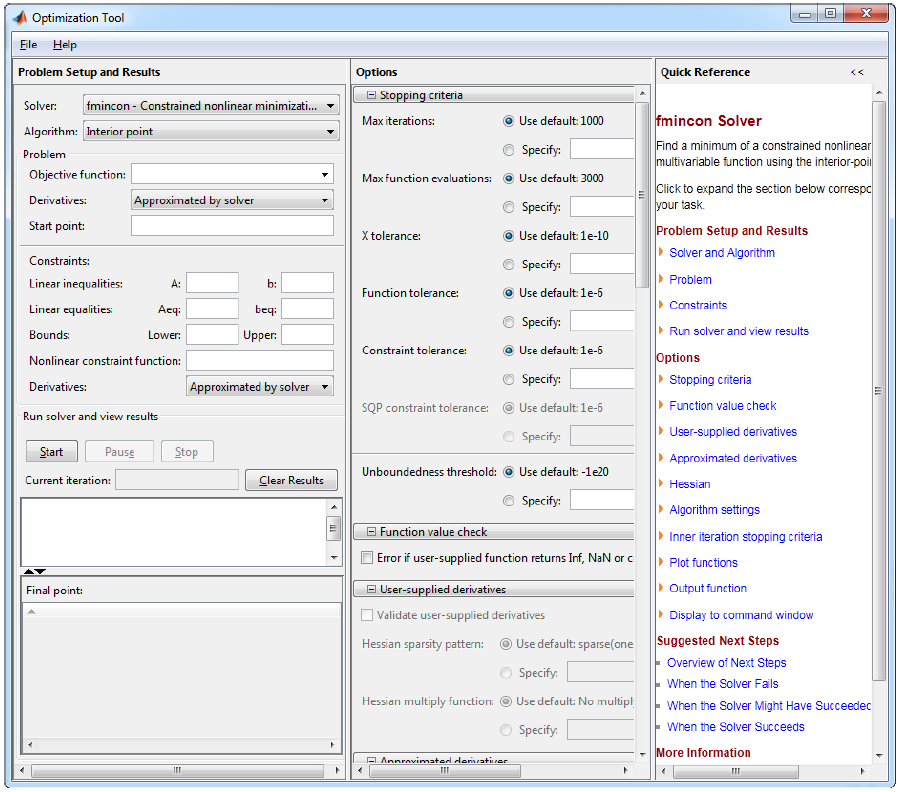
2.  همان طور که در تصویر بالا مشاهده می کنید، در گوشه ی سمت چپ و بالا، برای solver(حل کننده)مقدار fmincon - Constrained nonlinear minimization انتخاب شده است. این solver(حل کننده) برای این مسئله مناسب می باشد زیرا تابع روزن بروک غیرخطی می باشد و این مسئله دارای یک محدودیت می باشد. 

 3. در منوی Algorithm گزینه ی Interior point که پیش فرض است را انتخاب کنید. 

4. برای فیلد Objective function مقدار rosenbrock@ را وارد کنید. کاراکتر @ مشخص می کند که کلمه ی پس از آن، شناسه ی تابع در فایل rosenbrock.m است. 

 5. برای فیلد Start point مقدار [0 0] را وارد کنید. این یک نقطه ی ابتدایی است که حل کننده ی fmincon از آن شروع به جستجوی مینیمم می کند. 

 6. برای فیلد Nonlinear constraint function مقدار unitdisk@ را وارد کنید. این عبارت شناسه ی حل کننده ی unitdisk.m را تعیین می کند. 

 بنابراین بخش  Problem Setup and Results باید بصورت زیر تنظیم شده باشد: 

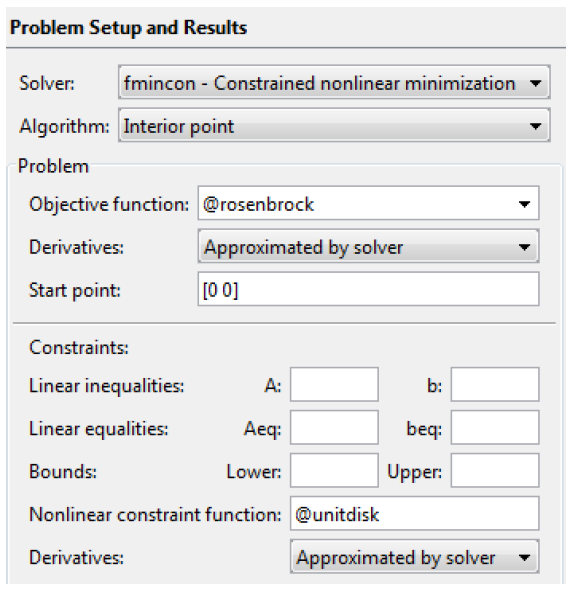
 7. در کادر(بخش) Options از منوی  Level of display گزینه ی iterative را انتخاب کنید. اگر این گزینه را مشاهده نمی کنید، بر روی Display to command window کلیک کنید. این کار باعث می شود که میزان پیشرفت حل کننده ی fmincon در پنجره ی command نشان داده شود. 

 8. حالا در زیر بخش Run solver and view results بر روی گزینه ی Start کلیک کنید. 

 پیغامی همچون زیر، در جعبه ی زیر دکمه ی Start به شما نشان داده خواهد شد: 

Optimization running.
Objective function value: 0.045674824758130374
Local minimum found that satisfies the constraints.

Optimization completed because the objective function is non-decreasing in 
feasible directions, to within the default value of the function tolerance,
and constraints are satisfied to within the default value of the constraint tolerance.

مقدار objective function که در پیغام بالا وجود دارد ممکن است برای شما کمی متفاوت باشد. زیرا به سیستم کامپیوتر شما و ورژن جعبه ابزار بهینه سازی بستگی دارد. 

این پیغام به ما می گوید که: 

• جستجو برای یافتن یک مقدار محدود شده ی مینیمم به پایان رسید زیرا مشتق تابع هدف در جهت های اجازه داده شده توسط محدودیت، تقریبا برابر با 0 است. 
• محدودیت مورد نظر به دقت لازمه رسیده است. 

مقدار x مینیمم کننده در بخش Final point نشان داده می شود. 

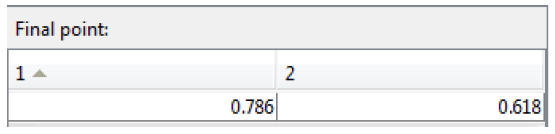
شما می توانید همین بهینه سازی را از طریق خط فرمان نیز بصورت زیر انجام دهید: 

 1. ابتدا برای انتخاب نمایش iterative و الگوریتم interior-point یک ساختار انتخاب گزینه ها را ایجاد می کنیم: 

options = optimoptions(@fmincon,...
'Display','iter','Algorithm','interior-point');

2. حالا حل کننده ی fmincon را اجرا می کنیم و ساختار انتخابی options را به آن می دهیم. حالا این حل کننده دو مقدار را برای ما برمی گرداند. بنابراین ابتدا موقعیت x  مینیمم کننده را در متغیر x قرار می دهد و سپس مقدار نهایی تولید شده توسط تابع هدف را در متغیر fval قرار می دهد:

[x,fval] = fmincon(@rosenbrock,[0 0],...
[],[],[],[],[],[],@unitdisk,options)

 در کد بالا، آن شش براکت خالی، درواقع محدودیت های اختیاری هستند که در این مثال به کار نمی آیند. برای مشاهده ی سینتکس این تابع، می توانید به مستندات تابع fmincon رجوع کنید. 

 خواهید دید که متلب یک پیغام را نشان می دهد و به دنبال آن، نتایج بهینه سازی را معرفی می کند:

Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the selected value of the function tolerance,
and constraints are satisfied to within the selected value of the constraint tolerance.
x =
0.7864 0.6177
fval =
0.0457

این پیغام به ما می گوید که: 

• جستجو برای یافتن یک مقدار محدود شده ی مینیمم به پایان رسید زیرا مشتق تابع هدف در جهت های اجازه داده شده توسط محدودیت، تقریبا برابر با 0 است. 
• محدودیت مورد نظر به دقت لازمه رسیده است. 

 تفسیر نتایج به دست آمده 

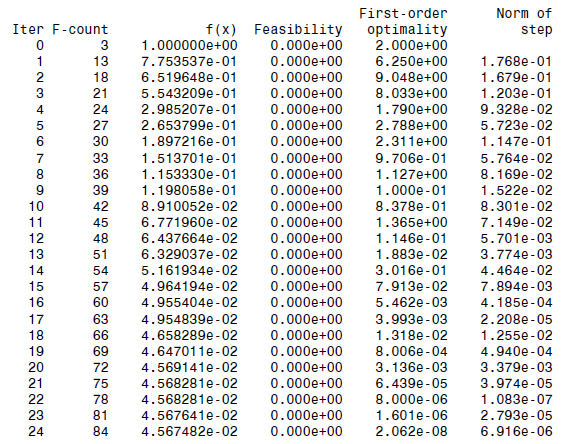
اگر به پنجره ی command نگاه کنید، یک سری اطلاعات بصورت یک جدول را مشاهده می کنید. ستون iteration در این جدول، نشان می دهد که متلب چگونه به جستجوی مقدار مینیمم تابع روزن بروک در دایره ی واحد، پرداخته است: 

 این جدول ممکن است با جدول شما کمی متفاوت باشد، زیرا به نسخه ی جعبه ابزار و پلتفرم شما بستگی دارد. در مورد جدول بالا، به نکات و موارد زیر توجه کنید:

• اولین ستون این جدول Iter نام دارد که تکرار را مشخص می کند و مقدار آن از 0 تا 24 است. بنابراین حل کننده ی  fmincon به تعداد 24 بار تکرار شده است. 
• دومین ستون، F-count نامیده شده است و تعداد کل دفعاتی که تابع روزن بروک اجرا شده است را نشان می دهد. در سطر آخر از ستون F-count عدد 84 را مشاهده می کنید. این عدد مشخص می کند که حل کننده ی fmincon برای پیدا کردن مقدار مینیمم، 84 بار تابع روزن بروک را اجرا کرده است. 
• سومین ستون (f(x نامیده شده است و مقدار تابع هدف را نشان می دهد. مقدار آخر این ستون ، یعنی مقدار 0.04567482 همان مینیمم گزارش شده در اپلیکیشن بهینه سازی(Optimization app) است. 
• چهارمین ستون Feasibility نام دارد و برای تمام تکرارها مساوی با 0 است. این ستون، مقدار تابع محدودیت unitdisk را در هربار تکرار نشان می می دهد تا جایی که محدودیت مثبت باشد. 

• قبلی
• بعدی