در این مقاله با موارد زیر آشنا خواهید شد:
- تبدیل یک مسئله به حالت حل کننده(Solver)
- تشریح مدل
- روش حل مسئله
تبدیل یک مسئله به حالت حل کننده
این مثال نشان می دهد که چگونه می توانیم یک مسئله را از حالت ریاضی به حالتی تبدیل کنیم که برای جعبه ابزار بهینه سازی متلب قابل درک و فهم باشد. در تمام مسائل خطی، این تکنیک برای حل کننده(solver) به کار می رود. متغیرها و عبارات این مسئله یک مدل در یک کارخانه ی شیمیایی را نشان می دهند.
توضیح مدل
فرض کنید که یک تابع به شکل زیر داریم:
تابع:
0.002614 HPS + 0.0239 PP + 0.009825 EP
در تابع بالا، کلمات HPS و PP و EP متغیر هستند و ما می خواهیم بر اساس محدودیت های زیر، مینیمم تابع بالا که تابع هدف نامیده می شود را پیدا کنیم:
محدودیت ها:
2500 ≤ P1 ≤ 6250
I1 ≤ 192,000
C ≤ 62,000
I1 - HE1 ≤ 132,000
I1 = LE1 + HE1 + C
1359.8 I1 = 1267.8 HE1 + 1251.4 LE1 + 192 C + 3413 P1
3000 ≤ P2 ≤ 9000
I2 ≤ 244,000
LE2 ≤ 142,000
I2 = LE2 + HE2
1359.8 I2 = 1267.8 HE2 + 1251.4 LE2 + 3413 P2
HPS = I1 + I2 + BF1
HPS = C + MPS + LPS
LPS = LE1 + LE2 + BF2
MPS = HE1 + HE2 + BF1 - BF2
P1 + P2 + PP ≥ 24,550
EP + PP ≥ 12,000
MPS ≥ 271,536
LPS ≥ 100,623
لازم به ذکر است که تمام متغیرهای بالا، مثبت هستند.
روش حل این مسئله
به منظور حل کردن این مسئله ی بهینه سازی، گام های زیر را به ترتیب در ادامه ی مقاله مطالعه کنید:
- انتخاب حل کننده(solver)
- قرار دادن متغیرها در داخل یک بردار
- نوشتن کران بالا و کران پایین محدودیت ها
- نوشتن محدودیت های خطی که بصورت نامعادله هستند
- نوشتن محدودیت های خطی که بصورت معادله هستند
- نوشتن و مشخص کردن تابع هدف
- حل مسئله با استفاده از حل کننده ی linprog
- امتحان کردن راه حل
انتخاب یک حل کننده یا solver
به منظور یافتن یک حل کننده ی مناسب برای این مسئله، به این مقاله (Optimization Decision Table) مراجعه کنید. چون که در مسئله، تابع هدف از نوع خطی است و همچنین محدودیت ها نیز از نوع خطی هستند، باید از حل کننده ی linprog استفاده کنیم.
همان طور که بعدا توضیح خواهیم داد، مسائل مربوط به حل کننده ی linprog به شکل زیر هستند:
$$\underset { x }{ min } { f }^{ T }x\quad \rightarrow \begin{cases} A.x\le b, \\ Aeq.x=beq, \\ lb\le x\le ub \end{cases}$$
\({ f }^{ T }x\) درواقع یک بردار سطری است که از یک سری ثابت f تشکیل شده است که در یک بردار ستونی از متغیرهای x ضرب شده است، و یا به عبارت دیگر به صورت زیر می باشد:
$${ f }^{ T }x=f(1)x(1)+f(2)x(2)+...+f(n)x(n)$$
به طوری که n نشان دهنده ی طول f است. ( یا به عبارت دیگر تعداد جملات f را نشان می دهد).
عبارت \(Ax\le b\) نشان دهنده ی نامعادلات خطی است. A یک ماتریس \(k\times n\) است به طوری که k، تعداد نامعادلات را نشان می دهد و n نیز تعداد متغیرها می باشد. b هم یک بردار با طول k است.
عبارت \(Aeq.x=beq\) نشان دهنده ی معادلات خطی است. Aeq یک ماتریس \(m\times n\) است، به طوری که m نشان دهنده ی تعداد معادلات است و n نشان دهنده ی تعداد متغیر ها است. beq نیز یک بردار با طول m است.
عبارت \(lb\le x\le ub\) به این معنی است که هر عنصر در بردار x باید از عنصر متناظرش در lb بزرگتر باشد و همچنین باید از عنصر متناظرش در ub کوچکتر باشد.
سینتکس حل کننده ی linprog به صورت زیر است:
سینتکس:
[x fval] = linprog(f,A,b,Aeq,beq,lb,ub);
قرار دادن متغیرها در یک بردار
همان طور که در توضیح مدل(در بالا) آمده است، ما در مدل خود، 16 متغیر داریم و باید آنها را در داخل یک بردار قرار دهیم. در کد زیر، با استفاده از آرایه ی سلولی، بردار مورد نظر را بصورت رشته ای ایجاد کرده ایم. هر یک از این رشته ها نام یک متغیر هستند:
بردار:
variables = {'I1','I2','HE1','HE2','LE1','LE2','C','BF1',...
'BF2','HPS','MPS','LPS','P1','P2','PP','EP'};
N = length(variables);
% create variables for indexing
for v = 1:N
eval([variables{v},' = ', num2str(v),';']);
end با اجرای دستورات بالا، متغیرهای زیر در workspace ایجاد می شوند:
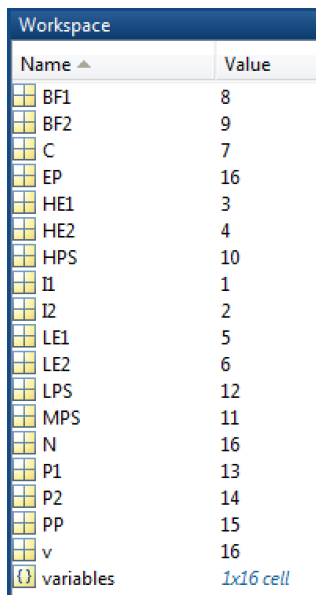
این متغیرهای نام گذاری شده، اندیس های عددی مولفه های بردار x را نشان می دهند. اما شما مجبور نیستید که این متغیرهای نام گذاری شده را ایجاد کنید.
نوشتن کران بالا و کران پایین محدودیت ها
در معادلات تعریف شده، چهار متغیر وجود دارند که دارای کران پایین هستند و 6 متغیر هم وجود دارند که دارای کران بالا هستند. متغیرهای دارای کران پایین عبارتند از:
کران پایین:
P1 ≥ 2500
P2 ≥ 3000
MPS ≥ 271,536
LPS ≥ 100,623
همچنین می دانیم که تمام متغیرها مثبت هستند؛ این یعنی کران پایین تمام متغیرها 0 هم است. پس ابتدا یک بردار کران پایین به نام lb ایجاد می کنیم و تمام عناصر آن را برابر با 0 قرار می دهیم و سپس آن چهار کران پایین دیگر(در کادر بالا) را به آن اضافه می کنیم:
دستور:
lb = zeros(size(variables));
lb([P1,P2,MPS,LPS]) = ...
[2500,3000,271536,100623];
متغیرهایی که دارای کران بالا هستند، عبارتند از:
کران بالا:
P1 ≤ 6250
P2 ≤ 9000
I1 ≤ 192,000
I2 ≤ 244,000
C ≤ 62,000
LE2 ≤ 142000
سپس برای ایجاد بردار حاوی کران های بالا، یک بردار می سازیم که تمام عناصر آن برابر با Inf (مثبت بی نهایت) باشند، و سپس شش کران بالا که در کادر بالا قرار دارند را به آن اضافه می کنیم(جایگزین می کنیم):
دستور:
ub = Inf(size(variables));
ub([P1,P2,I1,I2,C,LE2]) = ...
[6250,9000,192000,244000,62000,142000];
نوشتن محدودیت های خطی که بصورت نامعادله هستند
در معادلات ما( که در بالای مقاله آورده شدند) سه نامعادله وجود دارند، که عبارتند از:
نامعادلات:
I1 - HE1 ≤ 132,000
EP + PP ≥ 12,000
P1 + P2 + PP ≥ 24,550
به منظور اینکه این نامعادلات به شکل \(A.x\le b\) در بیایند، تمام متغیرها را به سمت چپ نامعادله ببرید. معادلات ما از قبل به این شکل در آمده اند. همچنین با ضرب کردن نامعادلات در عدد 1- کاری کنید تا علامت بزرگتری(<) در آنها به علامت کوچکتری(>) در بیایند.
نامعادلات:
I1 - HE1 ≤ 132,000
-EP - PP ≤ -12,000
-P1 - P2 - PP ≤ -24,550
در محیط workspace متلب، یک ماتریس به نام A با اندازه ی \(3\times 16\) ایجاد کنید به طوری که تمام عناصر آن صفر باشد. این ماتریس 3 سطر دارد برای سه نامعادله و 16 ستون دارد برای 16 متغیر. همچنین بردار b را نیز که سه مولفه دارد ایجاد کنید. به صورت زیر:
دستور:
A = zeros(3,16);
A(1,I1) = 1; A(1,HE1) = -1; b(1) = 132000;
A(2,EP) = -1; A(2,PP) = -1; b(2) = -12000;
A(3,[P1,P2,PP]) = [-1,-1,-1];
b(3) = -24550;
نوشتن محدودیت های خطی که بصورت معادله هستند
در بین معادلات ما، 8 معادله ی خطی وجود دارند، که عبارتند از:
معادلات:
I2 = LE2 + HE2
LPS = LE1 + LE2 + BF2
HPS = I1 + I2 + BF1
HPS = C + MPS + LPS
I1 = LE1 + HE1 + C
MPS = HE1 + HE2 + BF1 - BF2
1359.8 I1 = 1267.8 HE1 + 1251.4 LE1 + 192 C + 3413 P1
1359.8 I2 = 1267.8 HE2 + 1251.4 LE2 + 3413 P2
به منظور اینکه این معادلات به شکل \(Aeq.x=beq\) نشان داده شوند، تمام متغیرها را به یک سمت معادله می بریم. بنابراین معادلات ما به صورت زیر درمی آیند:
معادلات:
LE2 + HE2 - I2 = 0
LE1 + LE2 + BF2 - LPS = 0
I1 + I2 + BF1 - HPS = 0
C + MPS + LPS - HPS = 0
LE1 + HE1 + C - I1 = 0
HE1 + HE2 + BF1 - BF2 - MPS = 0
1267.8 HE1 + 1251.4 LE1 + 192 C + 3413 P1 - 1359.8 I1 = 0
1267.8 HE2 + 1251.4 LE2 + 3413 P2 - 1359.8 I2 = 0
حالا ماتریس Aeq و بردار beq را براساس معادلات بالا تشکیل دهید. برای انجام این کار، در متلب یک ماتریس به نام Aeq ایجاد کنید که ابعاد آن \(8\times 16\) باشد و از صفرها تشکیل شده باشد. 8 سطر برای 8 معادله و 16 ستون برای 16 متغیر. سپس برداری به نام beq که از 8 درایه(مولفه) تشکیل شده باشد را ایجاد کنید که از صفرها تشکیل شده باشد. به صورت زیر:
کد:
Aeq = zeros(8,16); beq = zeros(8,1);
Aeq(1,[LE2,HE2,I2]) = [1,1,-1];
Aeq(2,[LE1,LE2,BF2,LPS]) = [1,1,1,-1];
Aeq(3,[I1,I2,BF1,HPS]) = [1,1,1,-1];
Aeq(4,[C,MPS,LPS,HPS]) = [1,1,1,-1];
Aeq(5,[LE1,HE1,C,I1]) = [1,1,1,-1];
Aeq(6,[HE1,HE2,BF1,BF2,MPS]) = [1,1,1,-1,-1];
Aeq(7,[HE1,LE1,C,P1,I1]) = [1267.8,1251.4,192,3413,-1359.8];
Aeq(8,[HE2,LE2,P2,I2]) = [1267.8,1251.4,3413,-1359.8];
نوشتن و مشخص کردن تابع هدف
تابع هدف به صورت زیر است:
تابع:
f(x)= 0.002614 HPS + 0.0239 PP + 0.009825 EP
حالا عبارت بالا را بصورت بردار f می نویسیم:
بردار:
f = zeros(size(variables));
f([HPS PP EP]) = [0.002614 0.0239 0.009825];
حل مسئله با استفاده از حل کننده ی linprog
اکنون باید ورودی ها را به حل کننده ی linprog بدهیم. بنابراین این حل کننده را فراخوانی کنید و خروجی را بصورت زیر چاپ کنید:
حل:
[x fval] = linprog(f,A,b,Aeq,beq,lb,ub);
for d = 1:N
fprintf('%12.2f \t%s\n',x(d),variables{d})
end
fval
خروجی به صورت زیر خواهد بود:
خروجی:
Optimization terminated.
136328.74 I1
244000.00 I2
128159.00 HE1
143377.00 HE2
0.00 LE1
100623.00 LE2
8169.74 C
0.00 BF1
0.00 BF2
380328.74 HPS
271536.00 MPS
100623.00 LPS
6250.00 P1
7060.71 P2
11239.29 PP
760.71 EP
fval =
1.2703e+003
خروجی fval کوچکترین مقدار تابع هدف را در تمام نقاط امکان پذیر به ما می دهد.
بردار x نیز نقطه ای را نشان می دهد که تابع هدف در آن نقطه کمترین مقدار را دارد.
همچنین توجه کنید که:
- BF1 و BF2 و LE1 برابر با 0 هستند، یعنی برابر با کران پایین هستند.
- I2 برابر است با 244,000 یعنی کران بالا.
مقادیری از بردار f که برابر با 0 نیستند عبارتند از:
• HPS — 380,328.74
• PP — 11,239.29
• EP — 760.71






