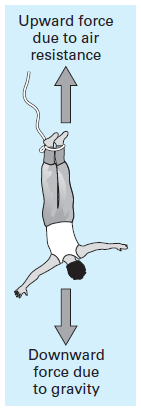
فرض کنید که یک شرکت وجود داشته باشد که خدمات سقوط آزاد با طناب انعطاف پذیر را ارائه می دهد و از شما درخواست می کند که سرعت سقوط آزاد اشخاص را به هنگام پرش، بصورت تابعی از زمان، محاسبه کنید.
این اطلاعات، به این شرکت کمک می کند تا بفهمد که طول طناب انعطاف پذیر و استحکام این طناب، باید برای اشخاص با وزن متفاوت چقدر باشد.
شما طبق اطلاعات قبلی خود از فیزیک، می دانید که شتاب، برابر است با نسبت نیرو بر جرم(قانون دوم نیوتن ).
بر اساس این قانون، و دانش شما از فیزیک و مکانیک سیالات، شما مدل ریاضی زیر را برای محاسبه ی نرخ تغییرات سرعت نسبت به زمان ارائه می دهید:
$$\frac { dv }{ dt } =g-\frac { { c }_{ d } }{ m } { v }^{ 2 }$$
در فرمول بالا، v مشخص کننده ی سرعت عمودی سقوط است و واحد آن \((m/s)\) است. و t مشخص کننده ی زمان است و واحد آن (s) است. g نیز شتاب گرانش را مشخص می کند که تقریبا برابر است با \((9.81m/{ s }^{ 2 })\) . نماد \({ c }_{ d }\) برابر است با یک ضریب پسار فشرده(lumped drag coefficient) و واحد آن \(kg/m\) است. متغیر m نیز وزن شخص رابه واحد kg مشخص می کند.
در اینجا به ضریب پسار، ضریب پسار فشرده گفته می شود زیرا این ضریب به عامل هایی همچون شکل بدن شخص و چگالی سیال بستگی دارد. (بخش 1.4 را ببینید).
به دلیل اینکه این معادله، یک معادله ی دیفرانسیل است، همان طور که می دانید ممکن است برای حل تحلیلی یا حل دقیق آن، به منظور به دست اوردن v بعنوان تابعی از t، به حساب دیفرانسیل و انتگرال نیاز باشد. اما در ادامه یک روش جایگزین برای حل آن، ارائه خواهیم داد.
در این روش، با استفاده از کامپیوتر، یک راه حل عددی یا تقریبی را ارائه می دهیم.
جدای از اینکه به شما نشان می دهیم که چگونه می توان با استفاده از کامپیوتر، این مسئله ی خاص را حل کرد، هدف کلی ما این است که موارد زیر را به شما نشان دهیم:
1) اینکه روش های عددی چه هستند.
2) اینکه چگونه می توان از این روش ها در حل مسائل علمی و مهندسی استفاده نمود.
همچنین در حین انجام این کار، روش استفاده از مدل های ریاضی را به شما نشان خواهیم داد.
یک مدل ساده ی ریاضی
به طور کلی، یک مدل ریاضی را می توان به صورت یک فرمول یا معادله تعریف کرد که ویژگی های ضروری یک سیستم یا فرآیند فیزیکی را به زبان ریاضی بیان کند. یک مدل ریاضی را به صورت کلی می توان بصورت یک رابطه ی تابعی، به شکل زیر ارائه داد:

(معادله ی 1.1)
مثال
نکته: تابع جبری یا forcing function چیست؟
در معادلات دیفرانسیل، به توابعی گفته می شود که تنها تابع زمان یا تنها تابع یک متغیر هستند و به جز آن، دیگر به هیچ متغیری وابسته نیستند. و به ازای هر مقدار t، یک ثابت هستند.
متغیر وابسته یک مشخصه است که معمولا رفتار یا حالت سیستم را بازتاب می دهد. متغیرهای مستقل نیز بُعد ها را مشخص می کنند مانند زمان و فاصله.
پارامترها نیز خاصیت های سیستم یا فرمول را نشان می دهند. توابع جبری نیز تاثیرات خارجی اعمال شده بر سیستم را نشان می دهند.
یک عبارت ریاضی واقعی از معادله ی 1.1 می تواند یک عبارت ساده ی جبری باشد و یا یک مجموعه ی پیچیده از معادلات دیفرانسیل باشد.
بعنوان مثال، نیوتن بر اساس مشاهدات خود، قانون دوم حرکت خود را فرمول بندی کرد. این قانون می گوید که نرخ زمانی تغییرات تکانه ی یک جسم برابر است با برآیند نیرو های اعمال شده بر آن.
بنابراین عبارت ریاضی یا همان مدل قانون دوم نیوتن با معادله ی زیر نشان داده می شود:
$$F=ma$$
به طوری که F نیروی خالص وارد شده بر بدن است(که واحد آن N یا \(kg\frac { m }{ { s }^{ 2 } } \) است). m نیز جرم جسم به واحد kg است. a نیز شتاب می باشد و واحد آن \(\frac { m }{ { s }^{ 2 } } \) است.
نکته:
نیوتن در کتاب اصول، قانون دوم حرکت خود را بر اساس مفهوم تکانه خطی بیان کردهاست:
برآیند همه نیروهای وارد شده بر یک ذره با نرخ تغییرات زمانی تکانه خطی ذره برابر است. بنابراین:
$$F=\frac { dp }{ dt } $$
می توانیم معادله ی 1.1 را با تقسیم دو طرف آن بر m به صورت زیر بنویسیم:
$$a=\frac { F }{ m } $$
(معادله 1.3)
در این معادله، a یک متغیر وابسته است و رفتار سیستم را مشخص می کند. F نیز وابسته به یک متغیر است(forcing function) و m هم یک پارامتر است. توجه کنید که در این مورد ساده، متغیر مستقلی وجود ندارد. زیرا ما هنوز پیش بینی نکرده ایم که شتاب چگونه در زمان یا فضا تغییر می کند. معادله ی 1.3 ویژگی های زیادی دارد و نمونه ای از مدل های ریاضی ارائه شده در جهان فیزیکی می باشد.
- این معادله، یک فرآیند یا سیستم طبیعی را به زبان ریاضی بیان می کند.
- این معادله واقعیت را به صورت آرمانی و به طور ساده نشان می دهد. زیرا این مدل، جزئیات ناچیز فرآیند طبیعی را نادیده می گیرد و تنها به ضروریات تکیه می کند.
بنابراین، قانون دوم نیوتون هنگام اعمال شدن بر روی اشیاء از تاثیرات کم اهمیت، تاثیر نمی پذیرد. - در نهایت، این معادله نتایج قابل تجدیدی را تولید می کند که بعدا می توانند مورد استفاده قرار بگیرند. بعنوان مثال، اگر نیروی وارده به یک شیء و جرم آن معلوم باشند، می توانیم از معادله ی 1.3 برای محاسبه ی شتاب استفاده کنیم.
به دلیل ساده بودن معادله ی 1.2 از نظر جبری، راه حل این معادله به سادگی انجام گرفت.
اما، دیگر پدیده های فیزیکی، که با مدل ریاضی نشان داده شده اند، حل آنها ممکن است خیلی پیچیده تر باشد. و یا اینکه ممکن است حل دقیق آنها امکان پذیر نباشد و یا به تکنیک های پیشرفته تر ریاضی نیاز داشته باشد.
برای مشاهده ی یک مدل پیچیده تر، می توانیم از قانون دوم نیوتون استفاده کنیم. می خواهیم به وسیله ی آن سرعت نهایی یک فرد در حال سقوط آزاد با طناب را در نزدیک محیط زمین محاسبه کنیم.
در این مورد باید شتاب را به صورت نرخ زمانی تغییرات سرعت(dv/dt) بنویسیم و در معادله ی 1.3 قرار دهیم تا نتیجه ی زیر حاصل شود:
$$\frac { dv }{ dt } =\frac { F }{ m } $$
(معادله 1.4)
در معادله ی بالا، v یعنی سرعت و واحد آن، متر بر ثانیه است. بنابراین نرخ تغییرات سرعت بر زمان، برابر است با نیروی خالص وارد شده بر بدن شخص تقسیم بر وزن آن.
اگر نیروی خالص مثبت باشد،حرکت جسم تند شونده است و اگر منفی باشد، حرکت جسم کند شونده است.
اگر نیروی خالص، برابر با 0 باشد، سرعت جسم ثابت باقی خواهد ماند.
حالا می خواهیم نیروی خالص را با استفاده از مولفه ها و پارامترها مشخص کنیم تا قابل محاسبه باشد.برای کسی که در نزدیکی زمین در حال سقوط است، نیروی خالص از ترکیب دو نیروی مخالف زیر به دست می آید:
- کشش جاذبه به سمت پایین(FD)
- فشار و مقاومت هوا به سمت بالا(FU)
بنابراین داریم:
$$F={ F }_{ D }+{ F }_{ U }$$
(معادله 1.5)
اگر به نیروی وارد شده به سمت پایین، علامت مثبت(+) اختصاص دهیم آنگاه می توانیم با استفاده از قانون دوم نیوتون، نیرو را با توجه به جاذبه، به صورت زیر بنویسیم:
$${ F }_{ D }=mg$$
(معادله 1.6)
مقدار g، شتاب جاذبه ی زمین است و مقدار آن (9.81m/{ s }^{ 2 }) می باشد.
مقاومت هوا را می توان از راه های دیگری به دست آورد. با استفاده از دانش مکانیک سیالات، متوجه می شویم که این فشار، به طور تقریبی متناسب است با توان دوم سرعت:
$${ F }_{ U }=-{ c }_{ d }{ v }^{ 2 }$$
(معادله 1.7)
به طوری که \({ c }_{ d }\) ضریب پسار نامیده می شود و و احد آن (kg/m) است. بنابراین هرچه سرعت سقوط آزاد بیشتر شود، نیروی مقاومت وارد شده توسط هوا به سمت بالا، بیشتر می شود. پارامتر \({ c }_{ d }\) به ویژگی های شیء در حال سقوط بستگی دارد. مثلا به شکل محیط آن جسم بستگی دارد. در مورد این شخص مثال ما که در حال سقوط آزاد است، پارامتر \({ c }_{ d }\) ممکن است به لباس یا جهت پرش فرد بستگی داشته باشد.
نیروی خالص، از تفاضل نیروی سمت پایین و نیروی سمت بالا به دست می آید. بنابراین معادله ی 1.4 می تواند با معادله ی 1.7 ترکیب شود تا نتیجه ی زیر حاصل شود:
$$\frac { dv }{ dt } =g-\frac { { c }_{ d } }{ m } { v }^{ 2 }$$
(معادله ی 1.8)
معادله ی 1.8 یک مدل است که شتاب یک شیء در حال سقوط را با نیروهای وارده به آن، مرتبط می کند.
این معادله، یک معادله ی دیفرانسیل است زیرا بصورت نرخ تغییرات (dv/dt) نسبت به متغیر مستقل تعریف شده است.
اما، برخلاف راه حل قانون دوم نیوتون(1.3) راه حل دقیق معادله ی 1.8 (در مورد سرعت سقوط آزاد) نمی تواند با استفاده از محاسبات جبری ساده به دست بیاید.
برای به دست آوردن جواب دقیق این معادله، باید از حساب دیفرانسیل و انتگرال استفاده کنیم. بعنوان مثال، اگر فرد پرنده، در آستانه ی پرش باشد(v = 0 در t = 0)می توانیم با استفاده از حساب دیفرانسیل و انتگرال، معادله ی 1.8 را برای حل کنیم. 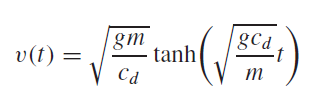
(معادله 1.9)
به طوری که tanh یک تانژانت هایپربولیک است که می تواند به طور مستقیم محاسبه شود و یا می تواند از طریق توابع نمایشی ساده تر مورد محاسبه قرار گیرد:
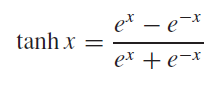
(معادله 1.10)






